2024-05-27 来源: 《银行家》2024年第5期
作者:叶永金 吴永政 兰 冰 汪 士
摘要:近年来,量子计算飞速发展,对众多行业,尤其是金融业产生变革性影响,外汇交易市场将是第一波受到量子科技冲击的金融市场。我们提出一种量子套利优化方法,将货币交换转化为二次无约束二值优化(QUBO)问题,利用量子退火算法,求解哈密顿量的最低能态,实现高效的套利分析。传统的套利算法求解最佳套利交易路径属于NP难问题,引入量子退火算法之后,极大地降低了计算的时间复杂度,为这一类问题的解决提供了一条可行的路径。该算法不仅可以得到最优解,还能求出所有有利可图的交易路径,让交易者在不同交易路径之间依据实际操作需要进行灵活选择。
关键词:套利;退火算法;量子计算
引 言
中共中央政治局于2020年10月16日下午就量子科技研究和应用前景举行第二十四次集体学习。中共中央总书记习近平在主持学习时强调,“当今世界正经历百年未有之大变局,科技创新是其中一个关键变量。要充分认识推动量子科技发展的重要性和紧迫性,加强量子科技发展战略谋划和系统布局,把握大趋势,下好先手棋”。随着量子科技时代的到来,量子计算、量子保密通信、量子测量等快速发展,其中量子计算以其超强的并行计算能力,不断突破传统计算的瓶颈,有望引领下一代科技革命。近几年,国内外量子计算得到快速发展,量子算法作为量子计算的应用方向,涉及各行各业,其中就包括在金融市场上的应用。本文聚焦量子算法在金融市场的创新研究,着眼量子科技的大趋势,下好量子金融的先手棋。
量子金融概述
金融市场每天产生海量的交易数据,如何快速而有效地处理,传统计算面临巨大挑战。量子计算以量子比特作为基础,利用量子比特的纠缠与叠加特性,表现出超强的并行计算能力,在一些特定问题的求解过程中, 有巨大的加速效果。比如Shor算法在大数的质因数分解过程中的指数级加速[1],Grover提出的查找算法,在无序集合查找问题上相对于经典算法的平方级加速[2]。于是人们希望将量子计算应用于金融领域,量子金融的概念产生,即量子计算在金融领域的应用。目前,量子计算在金融领域的应用主要集中于金融交易、风险评估和金融工程几个方向。量子计算在金融交易领域的应用为通过引入量子计算指导金融交易,主要包括证券投资组合优化、股票价格预测以及本文讨论的货币市场套利交易等。量子近似优化算法可以应用于证券投资组合,量子蒙特卡洛算法可以应用于股票价格预测,本文将量子退火算法应用于货币市场的套利交易。在风险评估领域主要是量子计算应用于信用评分和欺诈检测。有Daniel J.Egger提出信用评分的量子算法,Nouhaila Innan提出的量子图神经网络应用于欺诈检测[3]。量子金融工程主要指的是量子算法应用于金融衍生品的定价,其中包括期权定价等,量子蒙特卡洛算法也可以在这个方向发挥作用。
通过量子算法与金融市场的连接,将传统的金融问题,转化为特定的量子算法问题,利用量子计算机的特殊优势,突破传统计算的瓶颈,对于金融市场上的股票价格预测、投资优化组合、信用评估以及我们提出的外汇市场套利等金融问题,提供快速有效的解决方案。
量子退火算法与二次无约束二值优化问题(QUBO)
组合优化是在离散域或可简化为离散域内计算函数的最大或最小值。日常生活中存在各种组合优化问题,例如商旅问题、交通流量、班次规划等问题。此类问题通常包含非常多的可能解决方案,使得详尽的搜索变得棘手,因此需要寻求更加快速高效的计算方法。
为了克服这种计算限制,研究人员开发了一种被称为伊辛机的新型计算技术。伊辛机是求解伊辛模型问题的机器,即将特定的数学问题转化为伊辛模型的结构,构建该问题的哈密顿量,然后引入量子退火原理,让哈密顿量以绝热演化的方式,让系统从激发态逐渐向基态演化,寻找数学问题的最优解。许多利用伊辛机的研究已在各个领域进行:投资组合优化[4]、交通流量优化[5]、电子商务网站的项目列表优化[6]和材料设计[7]。本文将伊辛机的应用扩展到货币交易市场中的套利分析。
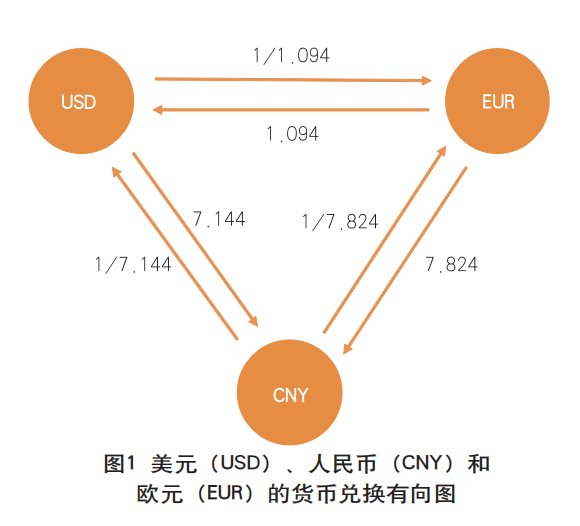
很多组合优化问题可以在数学上转化为伊辛模型或者QUBO的结构,利用伊辛机进行快速求解。伊辛模型和QUBO是通过图G(V, E)进行定义,其中V表示无向图顶点,E表示边。图1就是货币套利交易的图G(V, E)简单展示,节点(V)表示币种,边(E)表示币种之间的交易汇率,由于2个币种交易汇率不对称,所以该图是有向图。
伊辛模型
在图G(V, E)伊辛模型哈密顿量表达式为:
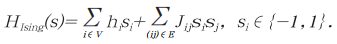
其中si是顶点i∈V上的自旋变量,hi是作用在i∈V 上的外磁场,Jij是边(i,j)∈E上的两个顶点之间的耦合强度。
二次无约束二值优化问题(QUBO)
QUBO表示的是二次无约束二值优化问题,损失函数仅由一次项和二次项组成,具体表达式为:
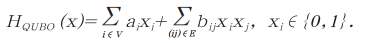
其中xi为第i个二元变量,ai和bij都为实数。通过与伊辛模型比较,可以看出伊辛模型中的二元变量取值为si∈{-1,1},QUBO的变量取值为xi∈{0,1},由于变量都是二元结构,伊辛模型和QUBO在本质上是一致的, 可以通过系数相互转换。
货币套利分析
货币套利指的是从不同市场上同一货币的不同价格交易中获利的方式。如图1所示,图中汇率为2023年11月27日的实时汇率数据,例如,100人民币兑换成美元,美元兑换成欧元,欧元再兑换成人民币,兑换后的人民币面值为100×(1/7.144)×(1/1.094)×7.824 ≈100.11,经过一个循环交易,人民币面值由100变为100.11,人民币面值升值了0.11%,说明这个循环有套利空间,相反则没有套利空间。
传统套利分析是通过套利检测算法实现,即通过定义如图2所示的有向图,对于有向图中的任意一个圆环,计算在该圆环内的汇率乘积,然后取对数,再乘以-1,即-log(ΠRij),其中Rij表示由币种i兑换成币种j的实时汇率,当(ΠRij)>1时,认为该循环内有利可图, 存在套利空间,相反则没有套利空间。在有套利空间的闭环中-log(ΠRij)的取值则为负数,简称负循环,套利检测算法就是搜索图中存在的负循环,并且在首次搜索到负循环之后就停止继续搜索。传统套利检测算法可以在多项式时间内解决,如使用时间复杂度为O(|V||E|) (其中|V|是节点数,|E|是边数)的Bellman-Ford算法,以及时间复杂度为O(|V|3)的F l oyd-Warsh all算法,这些算法的特点都是在首次发现负循环后就会终止搜索。相比之下,要找到最有利可图的套利机会,则需要对图内所有循环进行遍历搜索,遍历搜索的时间复杂度为O(|V|!),这属于NP难问题。
实际交易过程中,交易者会对交易模式更感兴趣,会综合考虑交易方式、市场流动性、更短的交易闭环、更少的风险等。例如,存在两个交易方案, 一个是微利,一个是暴利,一般传统的交易算法,如Bellman-Ford算法、Floyd-Warshall算法,在找到第一个有利可图的交易方案后就停止继续搜索。本文我们提供的量子退火算法,不仅可以找到最有利可图的交易方案,而且可以依据有利可图的顺序依次给出其他多个交易方案,供交易者在实际交易过程中选择最可行的交易路径。
对于一般情况,假设有N个币种,构建有N个节点(V),N×(N-1)条边(E)的有向图。用Rij表示由币种i兑换成币种j的汇率,实际交易过程中需要考虑汇兑交易中间费用,可以把居间费用成本折算进汇率中去, 本文由于仅讨论算法的有效性,暂不考虑居间成本。定义二元变量xij:
该优化问题的目标是希望找到有向图中最有利可图的交易闭环。即在一个闭环内,经过一次循环交易, 选取出ΠRij(闭环内所有的Rij)的最大值。对于更一般的表示,需要引入二元变量xij,即找出Π[ (Rij- 1 ) xij+1]的最大值,连乘在数学上可以通过取对数改为连加,所以我们的目标函数简化为:
由于我们交易必须是在一个闭环内完成,需要满足闭环的两个条件:首先,在图中的节点,如果在交易循环内,则会有一个货币兑换输入和一个货币兑换输出,数学上表达为:
如果图中的节点不在闭环中,则输入输出数都为0,上式也自动满足。其次,在图中的节点,如果在闭环内,则有且只有一个兑换输出,即满足,如果节点不在闭环内,则没有与任何其他节点的货币兑换,即满足,综合这两项得到第二个约束条件:
通过目标函数的确定和两个约束条件,就可以构建系统的目标哈密顿量。由于量子退火算法的固有特性是从激发态通过绝热演化寻找系统的基态,所以对上面的目标函数乘以-1,加入两个约束条件,得到该系统的哈密顿量为:
其中α和β为系统哈密顿量的超参数,取值为正数,当参数取值越大,在退火演化过程中约束性越强,具体数值在程序运行过程中,可以依据运行效率和结果进行适当调整。
确定了系统的哈密顿量,然后利用前面介绍的伊辛机去模拟量子退火过程,就可以快速求解出该系统的最低能态,即优化问题的最优解。
结果讨论
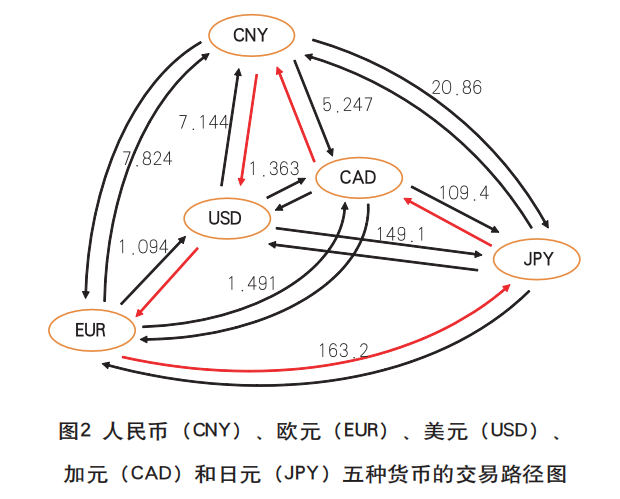
本文使用DWave公司开发的PyQUBO的模拟退火模块来实现量子退火模拟运算。根据前面的介绍,只要给出二元二次的哈密顿量,就可以通过PyQUBO完成量子退火的模拟计算。本文使用2023年11月27日的人民币、欧元、美元、加元和日元5种货币的实时汇率数据进行模拟计算输入,如图2所示。图中数字为当日的汇率,图中仅标示出了一半的汇率数据,另一半取倒数即可(如USD→CNY的汇率7.144,CNY→USD的汇率为1/7.144)。
通过量子退火算法的计算,该系统的最低能级对应的量子态就是我们需要的最优解结果。表1 列出了最低的五个系统能级,对应最优的5条交易路径,最优解在图2 中用红色箭头表示。表1 中的能量为系统哈密顿量所对应的能级。通过量子退火算法,我们找到了一条最有利可图的交易路径,即“JPY→CAD→CNY→USD→EUR→JPY”,通过该路径进行交易,一次交易闭环收益0.151%。该方法不仅可以提供最优交易路径,还给出其他交易路径,包含系统绝热演化过程中经历的所有交易路径,这里为了便于展示,仅列出收益前5的交易路径。所有有利可图路径的求解便于让交易者依据实际交易过程中的交易成本、市场流动性、更短的闭环等进行灵活选择。
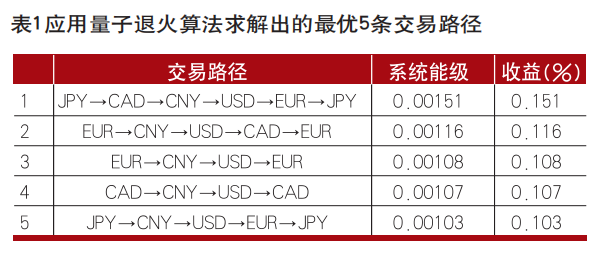
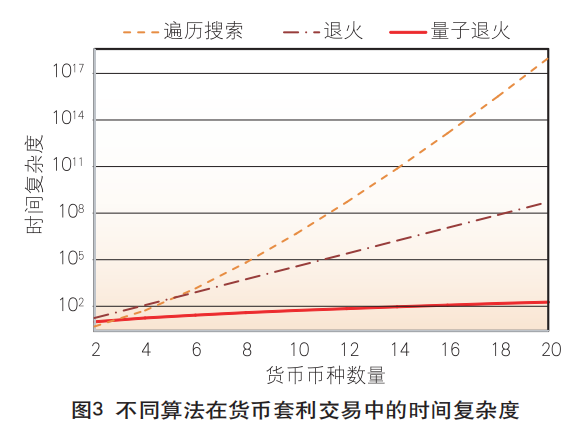
表1展示的是在5种货币中寻找出最有利可图的交易路径。实际的外汇交易市场有100多种主权货币,传统的套利检测算法在搜索到有利可图的交易路径之后就停止继续搜索,无法确保该路径是获利最多的一条交易路径,要寻找到最有利可图的交易路径需要遍历搜索,时间复杂度为O(N!),这属于NP难问题。由于Bellman-Ford算法与Floyd-Warshall算法在首次搜索到有利可图的循环之后就停止了搜索,搜索能力受到极大的限制。为了更好地展现量子退火算法的优越性,本文将具有相同搜索能力的遍历搜索、退火算法和量子退火算法进行了比较,其中退火算法和量子退火算法属于近似优化算法,退火算法的时间复杂度为O(eN),量子退火算法的时间复杂度为。图3展示的是三种算法的时间复杂度比较,由于三种不同的算法时间复杂度差异巨大,笔者对纵轴(时间复杂度)取了对数,随着被交易货币币种数量的增加,不同算法的时间复杂度变化有巨大的差异。通过比较可以看出,通过引入量子退火算法,时间复杂度显著下降,为解决传统NP难问题,提供了一条可行的路径。
结语
本文将量子退火算法的应用推广到货币交易市场,对传统NP难问题利用量子算法的超强并行计算能力进行解决,为货币交易市场打开了一扇新的大门。随着金融科技的发展,量子计算在金融领域的大量应用, 传统金融市场将会受到冲击,有些传统范围内无法解决的问题可能会被量子计算所突破,从而带来金融领域的全新变革。我们走在大时代的前沿,将量子科技引入金融领域,将会给我们带来一个崭新的金融世界。
【参考文献】
[1]S h o r PW.A l g o r i t h m s f o r Qua n t um Comp u t a t i o n : D i s c r e t e L o g a r i t h m s a n d Factoring [J]. Proceedings 35th Annual Symposium on Foundations of Computer Science, 1994:124-134.
[ 2 ] G r o v e r L K . A F a s t Q u a n t u m Mechanical Algorithm for Database Search [J]. Proceedings of the 28th Annual ACM Symposium on Theory of Computing, 1996: 212-219
[3]Nouhaila Innan, Abhishek Sawaika, Ashim Dhor, et al. Financial Fraud Detection using Quantum Graph Neural Networks[J]. 2023.
[4]G. Rosenberg, P. Haghnegahdar, P. G o d d a r d,e t a l. Sol v i n g t h e Opt i m a l Trading Trajectory Problem using a Quantum Anne a l e r[J]. I E E E J o u r n a l o f S e l e c t e d Topics Signal Processing, 2016, 10(6):1053- 1060.
[5]F. Ne u k a r t, G. C o m p o s t e l l a, C. Seidel,et al.Traffic Fow Optimization using a Quantum Annealer [J]. Frontiers in ICT, 2017, 4:1-6.
[6]N. N i s h i m u r a , K. T a n a h a s h i , K. Suganuma, et al. Item Listing Optimization f o r E - c o m m e r c e W e b s i t e s B a s e d o n Diversity[J]. Frontiers in Computer Science, 2019.
[7]K. Kitai, J. Guo, S. Ju, Tanaka, et al. Designing Metamaterials with Quantum Annealing and Factorization Machines[J]. P h y s i c a l R e v i e w R e s e a r c h, 2 0 2 0 , 2 ( 1 ): 0133191-01331910.
[8] M u k h e r j e e S , C h a k r a b a r t i B . Multivariable optimization: Quantum Annealing and Computation[J]. The European Physical Journal Special Topics. 2015. 224(1):17-24.
(作者单位:中国电子科技集团公司第三十二研究所)
责任编辑:张志敏